이번 포스트는 기존에 제가 평소에 다루던 주제와는 조금 다릅니다.
아니, 프론트엔드 개발자가 형식 언어와 컴파일러 얘기라니… 이 무슨 저-급(Low-Level) 레이어 이야기를 하고 계신건가요?
맞습니다. 사실 대부분의 개발자는 연구자가 아닌 이상 응용 소프트웨어를 만드는 일을 하지, 이렇게 컴퓨터 이론과 언어학 자체에 대해서 깊게 알 필요는 없는 것 같습니다. 그것보다는 비즈니스 로직을 잘 짜고, 효율적으로 코드를 작성하는 것이 중요합니다. 언어가 어떤 원리로 인식이 되고, 컴파일러가 어떻게 동작하는지의 지식은 업무 자체와는 크게 상관이 없습니다. 그런 지식들은 이미 누군가 에 의해 만들어진 극도로 최적화가 잘 된 기계와 컴파일러가 있고, 우리는 그들이 만든 환경 위에서 작업을 하게 됩니다.
그런데 저는 그들이 어떻게 이런 환경을 만들었는지가 궁금해졌습니다. 그렇지 않아도 올해부터 대학교에 복학을 하게 됐는데, 그 중에서도 컴퓨터 이론과 언어학에 대해 궁금한 게 있어서 관련된 강의를 듣고 있습니다. 그래서 이 글을 읽는 분들에게 어떻게 하면 이 지식을 재미있게 전달할 수 있을까 생각을 해봤습니다. 당장 몇 가지 익숙한 예시를 들어볼까요?
당장 멀리 가지 않더라도 TypeScript가 있습니다. TypeScript를 컴파일해서 나온 결과물이 JavaScript죠. 그런데 JavaScript는 브라우저에서 컴파일러에 의해 인식되는 것이 아니라 인터프리터(Interpreter) 에 의해 인식이 됩니다. 왜 TypeScript는 컴파일을 하는 것이고, 왜 JavaScript는 인터프리터로 인식할까요? 두 해석 방식의 차이를 이해하기 위해서는 컴파일 방법의 종류를 이해해야 합니다.
정규 표현식(Regular Expression) 도 많이들 쓰실 것입니다. 아시잖아요, JavaScript에서는 new RegExp() 로 시작하는 복잡하고 무시무시한 문법들. 이 문법들의 기초가 되는 것들 중 하나가 바로 형식 언어 이론에 포함되는 정규 표현식입니다.
우리가 프론트엔드 환경에서 작성한 모든 코드는 ESLint를 통해 최적화가 됩니다. ESLint는 내부적으로 추상 구문 트리(Abstract Syntax Tree)를 이용해서 우리가 문자열로 입력한 코드를 트리 형식으로 파싱하고, 이를 인식하여 구조를 파악합니다. 이 트리를 만드는 일은 컴파일러 내부를 구축하고 있는 파서(Parser) 가 주로 하는 역할입니다.
마지막으로 컴파일러 이론에서 사용되는 유한 상태 머신(Finite State Machine) 의 개념을 아예 프론트엔드에서 사용하는 예시도 있습니다. 바로 xstate라는 라이브러리입니다. 해당 라이브러리를 사용하면 복잡한 상태 관계를 선언적으로 설명하고, 다이어그램 또는 전이도(transition)를 이용해 쉽게 표현을 할 수 있습니다.
이처럼 형식 언어와 컴파일러 이론은 단순히 티가 나지 않을 뿐, 우리의 개발 환경 대부분을 만드는 데 있어 토대가 되곤 합니다. 그래서 오늘은 컴퓨터 이론의 기초가 되는 형식 언어와 컴파일러 이론에 대해 알아보도록 하겠습니다. 이번 포스트를 통해 컴파일러 이론에 대해 궁금하신 분 분들께 도움이 되기를 바랍니다.
TL;DR
- 우리가 작성한 코드는 컴파일러에 의해 토큰(token)으로 잘게 쪼개지고, 상관 관계를 가지는 트리로 만들어진 후, 어떤 기계에서 동작하는 기계어로 번역이 된다
- 이 때 토큰으로 잘개 쪼개는 부분을 어휘 분석기(또는 스캐너), 트리를 만드는 부분을 구문 분석기(또는 파서)라고 부른다
- 분석된 토큰을 일정한 규칙을 이용해서 요리조리 조립을 해야 하는데, 이 규칙을 형식 언어라고 부른다
- 형식 언어의 생김새에 따라 인식할 수 있는 언어에 차이가 있고, 이를 계층 관계로 나타낸 것이 촘스키 계층이다
- 어휘 분석기는 촘스키 계층의 3단계에 속하고, 구문 분석기는 촘스키 계층의 2단계에 속한다
그… 요약부터 상당히 길지만, 평정심을 잃지 않으셨으면 좋겠네요.
그래서 컴파일러가 뭔데?

우선 컴파일러 자체의 정의는 다음과 같습니다.
고급 언어로 쓰여진 프로그램을 어떤 특정한 컴퓨터에서 직접 실행 가능한 형태의 프로그램으로 번역해주는 컴퓨터 프로그램
인간이 컴퓨터에 일을 시키려면 컴퓨터와 인간이 서로 이해할 수 있는 공통적인 대화 수단이 필요합니다. 이러한 대화 수단을 언어(Language) 라고 합니다. 이 언어는 의사소통을 하는 대상이 누구냐에 따라 자연 언어(Natural Language) 와 형식 언어(Formal Language) 로 나뉩니다. 자연 언어는 한국어, 영어처럼 인간과 인간이 의사소통을 하는 언어로서 지역이나 민족에 따라 자연적으로 발생한 언어인 반면, 형식 언어는 인간과 기계 사이의 소통을 위해 인위적으로 만들어진 언어입니다.
기계는 일반적으로 저급 언어(Low-Level Language) 를 사용합니다. 기계가 사용하는 저급 언어 중 하나가 바로 0과 1로 구성된 기계어(Machine Language) 입니다. 하지만 인간이 기계어로 프로그래밍을 하기에는 너무 어렵고 복잡하다는 단점이 있죠. 그래서 이를 사람이 조금이라도 알아볼 수 있도록 개선한 언어가 바로 어셈블리어(Assembly Language) 입니다.
하지만 어셈블리어도 저급 언어의 수준을 벗어나지는 못했죠. 그 후, 저급 언어의 단점을 보완하기 위해서 인간의 가독성을 우선으로 여긴 인간 중심 언어가 나오게 되는데, 이를 고급 언어(High-Level Language) 라고 합니다. C(C도 경우에 따라서는 저급 언어로 분류되긴 합니다), Python, Java, C#, JavaScript 등 우리가 알고 있는 대부분의 언어가 고급 언어입니다.
이처럼 인간이 문제를 해결하기 위해서 컴퓨터와 의사소통을 하려면 위에서 이야기한 언어 가 필요합니다. 컴퓨터는 기계어를 사용하지만, 인간이 기계어를 사용하여 문제를 표현하기는 너무 어렵기 때문에 인간은 사람 중심 언어인 고급 언어를 사용합니다. 하지만 고급 언어는 컴퓨터가 이해하지 못하죠. 따라서 인간이 사용하는 고급 언어를 기계어로 변환해주는 번역기가 필요하고, 이것이 컴파일러입니다. 조금 더 이해하기 쉽게 비유하자면, 컴파일러는 마치 외국인과 대화를 하기 위해 필요한 번역기죠.
컴파일러는 번역기의 한 종류다

여기에서의 번역기는 하나의 프로그래밍 언어로 작성된 프로그램을 그와 동등한 의미를 가진 다른 프로그래밍 언어로 된 프로그램으로 변환하는 프로그램 입니다. 이와 같은 번역기의 종류로는 어셈블러, 컴파일러, 전처리기, 인터프리터가 있지만 그 중에서도 가장 대표적인 번역기가 바로 컴파일러죠. 그렇다면 다른 컴파일러와 다른 번역기 사이에는 어떤 차이가 있을까요?
인터프리터(Interpreter) 는 컴파일러처럼 전체 코드를 한 번에 기계어로 번역하는 것이 아니라, 언어의 코드를 한 줄씩 입력받아서 번역과 동시에 코드를 실행한 후, 그 결과를 출력하는 프로그램입니다. 인터프리터를 번역기로 사용하는 언어는 일반적으로 Python과 JavaScript 같은 언어가 있죠. 덕분에 프로그램의 수정이 용이하다는 장점이 있지만, 코드를 직접 실행시키기 전까지는 어떠한 문제가 발생할지 모른다는 문제가 있습니다. 때문에 최근에는 Python이나 JavaScript 같은 인터프리터 언어라고 하더라도, 개발 환경 자체에서 정적 분석 기능을 지원해주는 경우가 많죠.
전처리기(Preprocessor) 는 입력과 출력이 모두 고급 언어인 프로그램으로, 프로그래밍 언어에 유용한 기능들을 추가시킴으로써 언어를 확장시켜주는 역할을 합니다. 보통 프론트엔드에서는 전처리기로 CSS의 기능을 확장시켜주는 SASS를 많이 쓰곤 하죠. 때문에 기존의 CSS에서 사용할 수 없는 다양한 유틸 기능들을 SASS 전처리기를 적용함으로서 사용할 수 있습니다.
한편, 일반적인 컴파일러는 현재 자기 자신이 실행되고 있는 기계에서 실행할 수 있는 기계어로 번역하지만, 크로스 컴파일러(Cross Compiler) 는 자기 자신이 실행되고 있는 기계가 아닌 다른 기계에서 실행할 수 있는 기계어로 번역하는 컴파일러를 말합니다. 말이 복잡한데, 비유를 하자면… 한국인이 미국인과 영어로 의사소통하면서, 대화 내용을 일본인을 위해 일본어로 정리해준다고 하면 적절할 것 같네요.
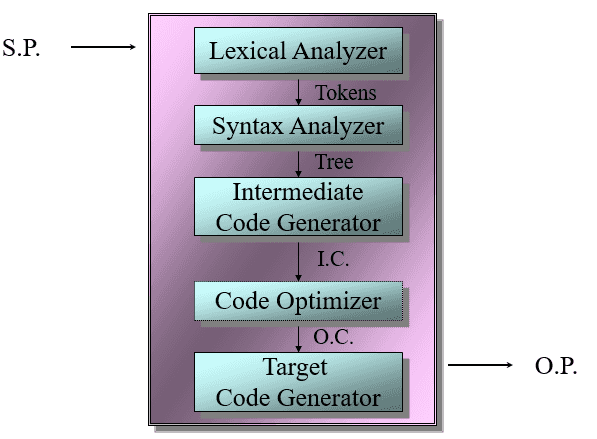
컴파일러 구조
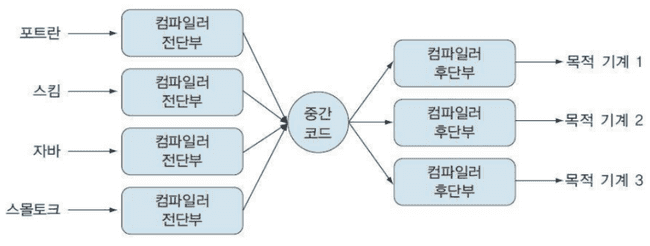
위에서 이야기한 컴파일러의 정의가 기억나시나요? 컴파일러는 입력과 출력이 있는 프로그램이고, 이를 논리적인 구조에 따라 전단부와 후단부로 구분할 수 있습니다. 전단부는 입력으로 받은 소스 프로그램을 후단부가 이해할 수 있는 코드로 번역하는 역할이고, 후단부는 해당 코드를 입력받아 동작시킬 기계에서 적합한 코드로 번역을 하는 역할을 담당하게 됩니다. 즉 전단부는 언어에 의존적이고, 후단부는 기계에 의존적이죠. 이 때문에 전단부는 후단부가 이해할 수 있는 별도의 코드를 결과물로 출력하는데, 이를 중간 코드(Intermediate Code) 라고 합니다.
컴파일러의 논리적 구조를 설명하기 위해, I am a boy라는 영어 문장을 한국어로 번역하는 과정을 살펴봅시다. 일반적인 사람들은 나는 소년이다 라고 직관적으로 해석할 수 있지만 컴퓨터는 자연어를 바로 해석할만큼 똑똑하지가 않습니다. 아마도 컴퓨터는 논리적인 연산 과정을 거쳐 다음과 같은 5단계를 거쳐 해석을 시작하겠죠.
- 문장에 사용된 단어를 검사 - 문장의 요소를 쪼개
I/am/a/boy라는 네 개의 단어를 확인 - 단어의 품사를 검사 - 각 단어가 명사, 대명사, 동사, 형용사, 부사, 전치사, 접속사, 감탄사 중 어디에 속하는지를 확인
- 각 단어가 문장에서 어떤 요소인지를 검사 - 각 단어가 주어, 동사, 목적어, 보어, 수식어 중 어디에 속하는지를 확인
- 문장 구성 요소 중 어디에 맞는지를 검사 - 문장이 몇 형식 문장인지를 확인
- 문법에 맞게 번역 - 한국어 단어 가운데 더 알맞은 단어로 번역
조금 복잡하지만, 컴파일러 역시 영어 문장을 번역하는 것과 비슷한 단계를 거칩니다.
어휘 분석
전단부의 첫 번째 단계인 어휘 분석기(Lexical Analyzer) 는 스캐너(Scanner) 라고도 불리며, 입력으로 들어오는 소스 프로그램을 읽어서 일련의 토큰(Token)을 생성하는 프로그램입니다. 여기에서 토큰은 프로그래밍 언어에서 문법적으로 의미를 갖는 최소한의 단위를 의미합니다. 마찬가지로 프로그래밍 언어에서도 if (a && b) 같은 코드를 [if, (, a, &&, b, )] 처럼 의미가 있는 단위로 잘게 쪼갭니다. 만약 $ 나 # 처럼 언어 자체에서 인식할 수 없는 토큰이 오게 된다면, 스캐너는 에러를 뱉게 됩니다.
구문 분석
전단부의 두 번째 단계인 구문 분석기(Syntax Analyzer) 는 파서(Parser) 라고도 불리며, 스캐너에서 출력된 토큰을 입력받아 코드의 구조를 나타내는 트리를 생성하는 프로그램입니다. 나타낼 수 있는 트리의 종류에는 파스 트리(Parse Tree)와 추상 구문 트리(Abstract Syntax Tree)가 있습니다.
중간 코드 생성
전단부의 마지막 단계인 중간 코드 생성 과정에서는 파서에서 출력된 트리를 바탕으로 변수의 타입 같은 검사를 실행하고, 중간 코드(Intermediate Code) 를 생성합니다. 이 중간 코드로 사용되는 것들의 예시가 U-Code, Java의 바이트 코드입니다.
바로 최종 결과물을 만들지 않고 중간 코드를 또 따로 만드는 이유는 무엇일까요? 바로 언어와 기계 사이의 의존성을 독립적으로 유지하기 위해서입니다. 만약 중간 코드를 만들지 않고 컴파일러가 바로 기계어를 생성한다면, 해당 컴파일러는 해당 기계에서 특정한 언어만 인식할 수 있는 컴파일러가 될 것입니다. 하지만 중간 코드를 생성함으로서 이 언어를 파싱하면 무조건 이런 결과물이 나오니, 이와 동치인 기계어를 생성하는 것은 기계와 가까운 후단부에게 맡기는 형태가 됨을 알 수 있습니다.
코드 최적화
여기서부터는 후단부 과정입니다. 코드 최적화(Code Optimization) 단계에서는 코드의 전단부에서 생성된 중간 코드를 바탕으로 비효율적인 코드를 찾아 코드 최적화 단계를 실시합니다. 최적화 단계는 크게 로컬 최적화(Local Optimization)과 전역 최적화(Global Optimization)으로 구분됩니다.
로컬 최적화 단계에서는 다음과 같은 최적화를 진행합니다. 실제로도 상당한 수준의 코드 최적화를 실제로 획득할 수 있습니다.
- 상수 연산(Constant Folding):
a = 2 * 3 * 4같은 식을a = 24로 치환 - 상수 전파(Constant Propagation):
a = 5, b = a + 5같은 식을a = 5, b = 10으로 치환함 - 불필요한 로드와 중복을 제거
- 식의 대수학적 간소화(Algebraic Simplification)
- 연산 강도 경감(Strength Reduction): 시간이 많이 소요되는 연산을 시간이 적게 걸리는 연산으로 대치함
한편 전역 최적화 단계에서는 다음과 같은 최적화를 진행합니다.
- 공통 부분식 축약(Common Subexpression Elimination)
- 반복문 내에서 값이 변하지 않는 코드를 밖으로 이동시키는 코드 이동
- 도달할 수 없는 코드를 삭제
목적 코드 생성
최적화가 진행된 중간 코드를 바탕으로, 마지막 단계에서는 목적 기계에서 동작하는 코드를 생성합니다. 여기서부터는 하드웨어에 의존적인 작업들이 진행됩니다.
컴파일러를 만드는 컴파일러
지금까지는 언어를 입력으로 받아 언어를 출력하는 컴파일러에 대해 알아보았는데요, 세상에… 컴파일러를 생성하는 컴파일러도 있습니다. 기술의 발전에 따라 고급 언어와 기계의 종류가 늘어나는만큼, 실제로 해당 고급 언어를 기계에서 동작시키기 위해서는 고급 언어의 개수 * 기계의 종류 개 만큼의 컴파일러가 필요합니다. 따라서 이 과정을 자동화하기 위해 똑똑하신 분들이 컴파일러를 생성하는 컴파일러를 만들었고, 이 이름이 컴파일러-컴파일러(Compiler-Compiler) (…)입니다.
위에서 이야기했던 컴파일러의 각 단계를 자동으로 만들어주는 도구도 있습니다. 스캐너를 생성하는 도구인 LEX, 파서를 생성하는 도구인 YACC, BISON 등이 있습니다.
언어
우리가 여태껏 컴파일러에 대해 이야기를 한 이유는 바로 언어를 인식하는 원리와 과정에 대해 알고 싶기 때문입니다. 그렇다면 언어를 어떻게 정의할 수 있을까요? 바로 그 규칙을 정의하면 됩니다. 이렇게 규칙이 잘 정의된 언어를 형식 언어(Formal Language) 라고 부릅니다.
언어에 대한 기본 규칙은 아마 정규표현식을 써보셨다면 익숙한 기호들이 있을 것입니다. 하지만 낯선 용어 자체도 많으니, 조금 더 자세히 살펴보겠습니다.
알파벳(Alphabet) 은 심벌(Symbol)의 유한집합니다. 우리가 알고 있는 영어의 알파벳과는 약간 다른 개념인데, 언어에서 인식할 수 있는 최소한의 의미를 가지는 단위를 심벌이라 하고, 이것들의 집합을 알파벳이라 합니다.
- 일때 생성되는 스트링 는
스트링(String) 은 알파벳으로부터 생성된 심벌의 유한수열입니다. 이 스트링을 연산하기 위한 연산자들이 아래에 정리되어 있습니다.
- 절대값 기호는 스트링의 길이 (즉, 일 때, )
- 은 스트링의 길이가 0인 스트링,
- 이 총 개
- 은 a에
reverse연산을 한 스트링 (즉, )- 는 a가 1개 이상 반복되어서 만들어질 수 있는 스트링 (즉, )
- 는 a가 0개 이상 반복되어서 만들어질 수 있는 스트링 (즉, )
아니… 그래서 갑자기 이 복잡한 수식이 나온 이유가 뭔데?
갑자기 머리 아픈 수식이 나온 이유는 언어의 정의를 표현하기 위해서입니다. 언어 은 알파벳 로부터 만들어질 수 있는 모든 스트링들 의 부분집합입니다. 그리고 어떤 언어에 속하는 스트링을 문장(Sentence) 이라고 부릅니다.
참고로 언어끼리의 연산도 있는데, 위와 비슷한 원리로 연산이 적용됩니다.
문법
위에서 언어를 구성하는 스트링에 대해 알아보았습니다. 이제 이렇게 만들어진 언어들을 표현하기 위해서 여러 수학 기호를 이용해 표시하는데, 이게 참 괴랄합니다.
- : 논터미널 심벌의 유한 집합
- : 터미널 심벌의 유한 집합
- : 생성 규칙의 유한 집합
- : 시작 심벌
좀 징그럽게 생겼지만 천천히 설명해볼게요. 우선 는 형식 문법을 정의하는 방법이고, 네 개의 파라미터를 받는다고 생각하면 됩니다. 그 파라미터에 좀 여러가지 복잡한 것들을 집어넣죠.
은 논터미널 집합이라고 부릅니다. 쉽게 말해, 수학에서의 매개변수와도 비슷합니다. 우리가 수학 문제를 풀 때, 공통되는 부분을 매개변수로 치환해서 풀 때가 있습니다. 그런데 그 매개변수를 실제 해를 구할 때 출력하지는 않죠. 마찬가지로 논터미널 집합은 시작 심벌에서 시작해서 이런저런 과정을 거쳐 최종적인 상태를 출력하기 위해 임시로 선언하는 변수라고 생각하면 편할 것 같습니다. 일반적으로 논터미널 집합은 영대문자로 구성이 되어 있습니다.
는 터미널 집합이라고 부릅니다. 터미널 집합은 언어를 구성하고 있는 단위들의 집합입니다. 논터미널 집합이 매개변수라면, 터미널 집합은 실제로 언어를 구성하고 있는 해입니다. 일반적으로 논터미널 집합은 영소문자로 구성이 되어 있습니다.
는 생성 규칙입니다. 생성 규칙은 집합으로 표현된 것이 아니라 별도의 표로 구성되어 있는데요, 일반적으로 아래와 같이 생겼습니다. 좀 더 전문적인 말로 표현하자면 상태 전이도(State Transition Table)와 거의 비슷합니다.
완전하게 이해가 가진 않겠지만, 대충 화살표의 모양을 보아하니 왼쪽의 상태가 오른쪽으로 진행되어야 할 것처럼 생겼습니다. 그리고 놀랍게도 그게 맞습니다. 한편 위에서 얘기했듯이 와 는 대문자로 구성되어 있으니 논터미널 집합에 포함이 되고, 와 는 터미널 집합에 포함이 되나 봅니다. 기호는 OR 연산이라고 생각하면 됩니다. 라는 상태에서, 로도 갈 수 있고, 로도 갈 수가 있다는 뜻이죠.
는 시작 심벌입니다. 쉽게 말해서 내가 에 있는 규칙을 따라 이렇고 저렇게 상태를 이동시킬 건데, 그 시작을 부터 하면 좋겠다는 뜻입니다.
이렇게 정의한 문법을 라고 부르겠다는 것이고, 이 문법으로부터 생성된 일련의 규칙들을 가진 언어를 라고 표현합니다. 즉, 문법 가 주어졌을 때 는 시작 심벌로부터 유도될 수 있는 모든 문장들의 집합을 의미하며, 이것이 언어와 문법의 관계입니다.
위에서 예시로 든 문법의 생성 규칙으로 만들어지는 언어를 들여다보면 아래의 규칙을 찾을 수 있습니다.
- = , , , , …
근데 주어진 문법으로 생성되는 언어를 찾는 과정은 특별한 규칙이 없기 때문에 어느 정도 노가다를 해야 합니다. 예시는 좀 쉬운 것으로 들긴 했지만, 규칙이 복잡해진다면 심히 어렵습니다. 그래서 규칙으로부터 유도될 수 있는 문장들을 길이가 짧은 순서대로 구하고, 그것들 사이의 규칙을 구하는 것이 그나마 나은 방법이 될 수 있습니다.
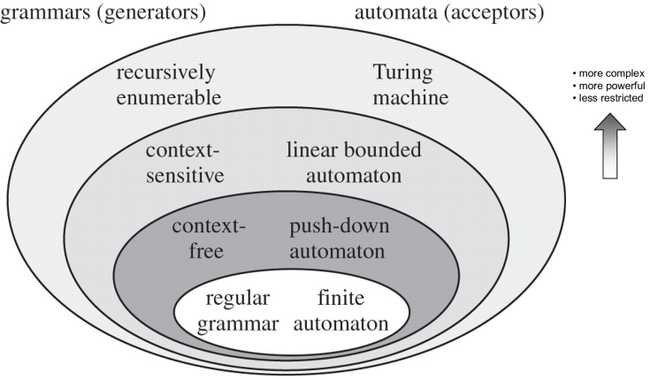
촘스키 계층
위에서 이야기한 문법의 개념은 언어학자인 노암 촘스키에 의해 소개된 것입니다. 촘스키는 생성 규칙이 일부 규칙에 따라서 계층 관계를 나누었는데, 이를 촘스키 계층(Chomsky Hierarchy)이라고 부릅니다.
- 제0유형: 무제약 문법(UG, Unrestricted Grammar)
- 생성 규칙에 별도 제약 없음, 다만 좌변은 이 될 수 없음
- 튜링 머신으로 인식됨
- 제1유형: 문맥 의존 문법(CSG, Context-Sensitive Grammar)
- 생성 규칙의 좌변이 , 우변이 일 때 여야 함
- 단, 언어의 정의에 따라 우변에 이 예외적으로 포함됨
- 선형 구속 오토마타에 의해 인식됨
- 제2유형: 문맥 자유 문법(CFG, Context-Free Grammar)
- 생성 규칙이 , , 형태를 가짐
- 푸시 다운 오토마타에 의해 인식됨
- 제3유형: 정규 문법(Regular Grammar)
- 생성 규칙이 (우선형 문법) 또는 (좌선형 문법) 형태를 가짐
- 유한 상태 오토마타에 의해 인식됨
규칙을 잘 살펴보시면 유형이 높아질수록 규칙이 엄격해지는 것을 알 수 있습니다. 이를 계층 관계로 나타낼 수 있으며, 계층 관계가 깊어진다는 것은 그보다 낮은 단계의 제약 조건을 모두 만족한다는 것을 의미합니다. 만약 생성 규칙 중에 제2유형, 제3유형을 만족시키는 규칙이 있다면 제2유형으로 인식이 됩니다.
이러한 정규 문법은 오토마타, 그리고 정규 표현식의 다른 방법으로도 표현할 수 있습니다. 오토마타와 정규 표현식은 양이 방대한만큼, 지금 당장 다루지는 않습니다.
…그래서 이게 컴파일러랑 무슨 상관인데?
컴파일러의 첫 단계인 어휘 분석기는 위의 정규 문법을 따르기 때문에 오토마타를 이용해 구현되어야 하기 때문입니다. 아마 실제 예시를 봐야 이해가 빠를 것 같습니다.
일반적으로 우리가 변수를 선언할 때에는 다음과 같은 규칙을 따라야 합니다.
- 변수의 이름 길이는 한 글자 이상
- 변수의 이름에는 영어, 숫자, 언더스코어(
_)(, 그리고 일부 언어에서는 유니코드 캐릭터까지)가 사용될 수 있음- 하지만 변수의 첫 글자에는 숫자가 올 수 없음
이는 명확하게 정해진 규칙이고, 이를 약속된 정규 문법으로 나타내면 다음과 같습니다.
- : : 임의로 만든 두 개의 논터미널
- : : 논터미널을 이용해 인식할 터미널
- :
- :
에서 출발하여, 처음에는 무조건 영어와 언더스코어만 올 수 있고, 그 이후부터는 영어, 언더스코어, 숫자가 제한없이 반복해서 올 수 있다는 문법을 위와 같이 나타냅니다. 이 식을 각각 오토마타와 정규 표현식으로 나타내면 다음과 같습니다.
우리는 자연어로 표현된 규칙을 위와 같은 방법으로 선언하여 어휘 분석기에게 토큰을 인식할 방법을 알려 줄 수 있습니다. 비슷한 방법으로 컴파일러의 다른 부분을 만들고, 이들을 결합한 후 특정 기계에서 돌아가는 기계어로 번역을 하게 만들면 됩니다.
마무리
여기까지 해서 간단하게 컴파일러, 그리고 형식 언어와의 관계를 알아보았습니다. 내용이 다소 복잡하지만, 둘 사이의 관계 이해에 조금이라도 도움이 되었기를 바라면서 글을 마치겠습니다.